This post is part of a series where I'm hoping to prove to myself that building a dynamic website with NodeJS is much more fun than using a CMS platform. See the first post for an explanation of why

The code can be found on GitHub

Previous Post

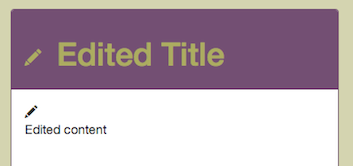
In the last post I wasn't happy with the visual affordance that a page element is editable.

I also wasn't happy that the page elements shifted around as alerts were added to the screen.

So…

That's what a proof of concept is for, right?

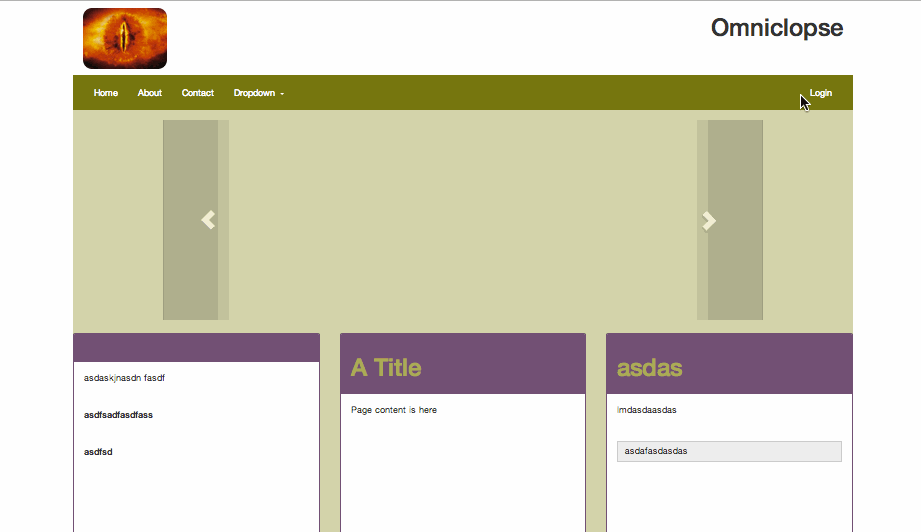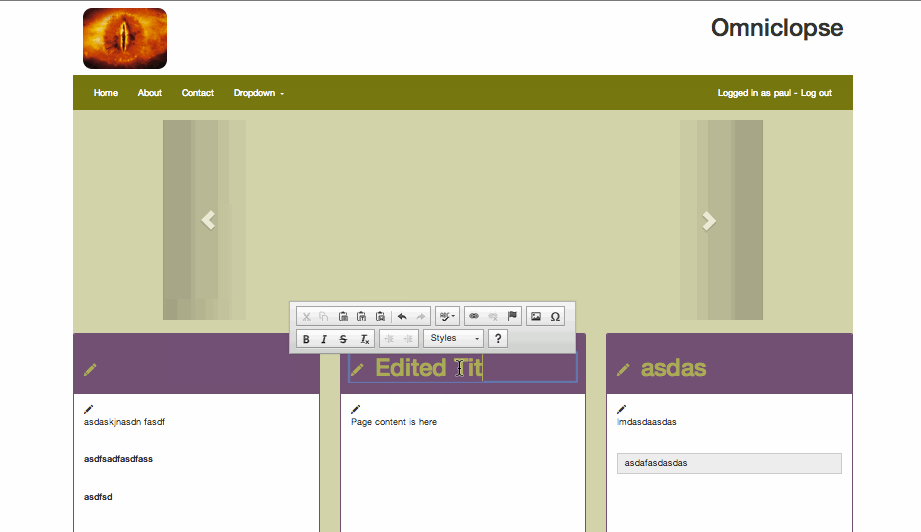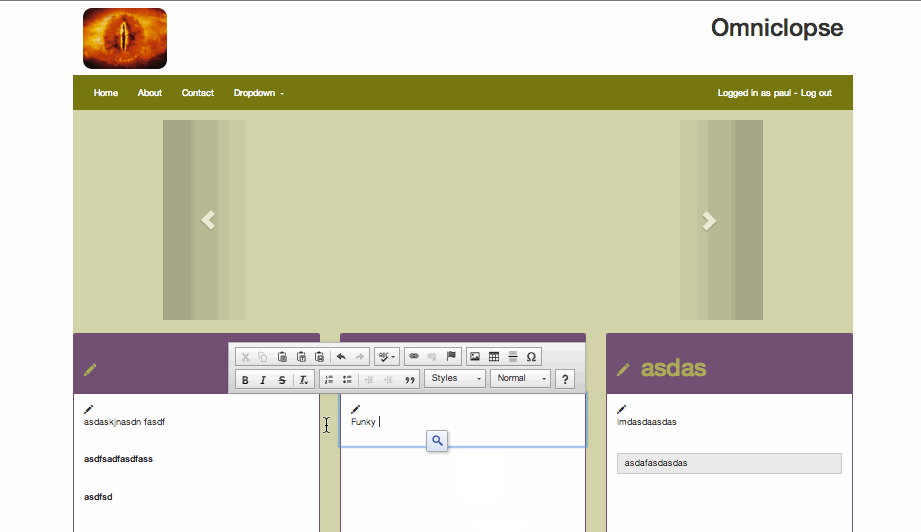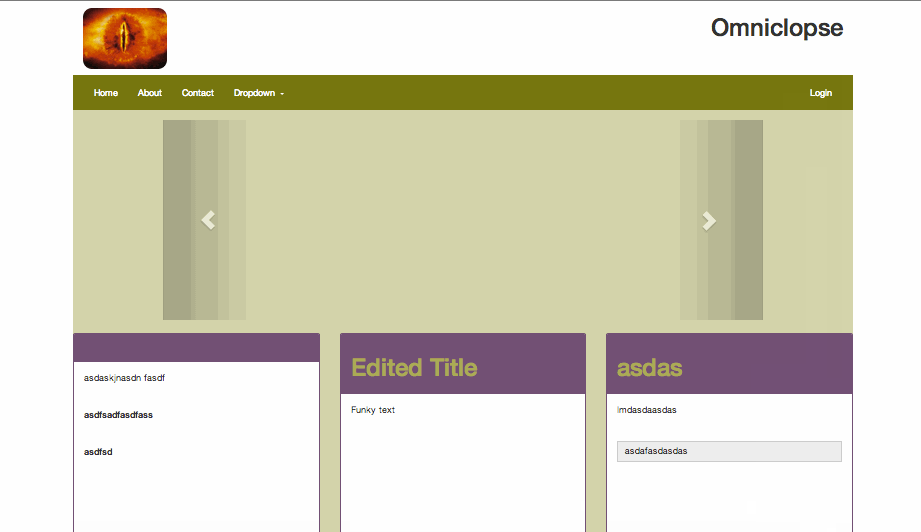
I still don't have a better idea of how to indicate that an element is editable but we can make it nicer!

And…

There are two steps

• Make the affordance more betterer
• Make the affordance give more info

A more affordable affordance

_{ouch! what a pun}

The indicator that an element is editable has to be on the element itself otherwise how is a user to know what they can edit - but what we had didn't draw the eye.

By using CSS3 keyframes we can cock-a-snoot at older browsers (without breaking them) and get the desired behaviour.

@mixin editorAffordance($size, $pos, $glow) {
  position: absolute;
  left: $pos;
  top: $pos;
  z-index: 900;
  color: $glow;
  font-size: $size;
  border-radius: 15px;
  padding: 5px;
}

[contenteditable] {
  -moz-user-select: none;
  -khtml-user-select: none;
  -webkit-user-select: none;
  -ms-user-select: none;
  user-select: none;
  outline: none;
  position: relative;
}

div[contenteditable] {
  .editable-affordance {
    @include editorAffordance(1em, 0, $complementaryDarkTwo);
    @include animation("darkpulse 2.5s infinite ease-in");
  }
}

h1[contenteditable] {
  .editable-affordance {
    @include editorAffordance(0.5em, -0.5em, gold);
    @include animation("goldpulse 2.5s infinite ease-in");
  }
}

The important bits here are:

The positioning

Using the [contenteditable] rule to set position:relative on the editable elements means we can add an element as a child with .editable-afforance as one of its classes. That class has a rule that sets position:absolute and some positioning to put the element top left (but those positions are passed in so don't need to be top left).

Positioning something absolutely inside something that is positioned relatively positions the child in relation to the parent (see - CSS is straight-forward ).

Giving an element that indicates something is editable but doesn't push that editable content out of its way.

No blue outline

Adding user-select:none means that when the editable element is selected the browser doesn't (shouldn't?) add its default outline that indicates the item is selected.

The magic

The @include animation('dark pulse... is where the magic happens.

The animation.scss file has some scss goodness that pumps out browser specific versions of the rules required for the pulse effect. That complexity also hides what's going on somewhat.

As always the Mozilla Developer Network documentation is awesome. In (very) short the animation rule is passed the name of a keyframes rule. The keyframes rule tells the browser what CSS to apply at known points in the animation. Those known points are calculated using the animation duration.

So, if 2s is set as the animation-duration then a keyframe rule for 50% applies after 1 second.

Here there are three rules that set a cycling box shadow inside and outside of the element

@include keyframes(darkpulse) {
  0% {
    box-shadow: inset 0px 0px 5px rgb(61, 28, 79), 0px 0px 15px rgb(61, 28, 79);
  }
  50% {
    box-shadow: inset 0px 0px 15px rgb(61, 28, 79), 0px 0px 35px rgb(61, 28, 79);
  }
  100% {
    box-shadow: inset 0px 0px 5px rgb(61, 28, 79), 0px 0px 15px rgb(61, 28, 79);
  }
}

And here is a codepen so you can play with the CSS that generates the effect

See the Pen gIseG by Paul D'Ambra (@pauldambra) on CodePen.

The next post will cover the second objective of making the editable affordance give information about whether saving edits was successful.